
中学校からは、小学校とはちがう新しい勉強が始まります。算数は数学という教科に変わりますし、英語の勉強もより本格的にスタートします。どんな心構えでいたらいいのか、不安に思っている人もいると思います。そんなみなさんに、英語や数学を勉強するときの心構えや、楽しく勉強を続けるアイデアなどを紹介します。


私は普段、月刊誌の編集の仕事をする傍ら、会社が運営する中高生対象の数学単科ゼミに出講しています。授業を通してじかに生徒さんと接していると、雑誌を黙々と編んでいるだけでは得られない「貴重な経験」をすることがあります。
私の担当は、中学1年生のクラス。中学受験を終えた子どもたちが多く集まるクラスです。ある回の授業のテーマは“対応付け”。主に、「場合の数を工夫して求めましょう」という内容です。
「ある一定のエリアに住む人の数を“人口”というよね。なぜ、“人口”というのか、知ってる?」という問いかけから始まります。「昔の中国では人の数を“一口、二口、…”と数えていたんだ。鉛筆を“一本、二本、…”と数えるようにね。それが由来なんだけれど、ここでは、少し違った見方をしてみよう」ハナシは本題へ。「人の数と口の数は、一致するよね。だって、一人の人には口が一つ付いているから。…ということは、人の数を知りたければ、口の数を数えればいいんだ」そして、「今日はそんなおハナシ。○○の場合の数を数えたいのだけれど、言い換えると、△△の数を数えることと同じだから、△△の方を数えちゃおう!
…その言い換えを“対応付け”と呼んでいるんだ。」
この授業で、次の問題を扱いました。紙上では、やや省略気味に進めます。
円周上に異なる10個の点があります。これらのうち2点を結ぶ直線(円外にも伸びる)をすべて引いたところ、どの2本も1点で交わり、どの3本も1点では交わりませんでした。このとき、円の内部はいくつの領域に分かれますか。
ほどなく、手が挙がりました。
(生徒A)「この問題、知ってます!小学生のとき、塾で公式を教わりました。
“(㋐直線の本数)+(㋑円の内部にできる交点の数)+1”で答えは出ますよね!」
なんと!中学受験の塾ではこんなことまで教えるのか!と驚きつつも、「えぇ、ホントに?…じゃ、ちょっとその公式とやらを使ってやってみよっか」
「㋐は10個の点から2個を選び、それを結べば1本の直線が引けるから、直線の本数は、10個の点から2個を選ぶ選び方、つまり“10個から2個を取る組み合わせ”に等しいね。これぞ対応付け(!)だ。
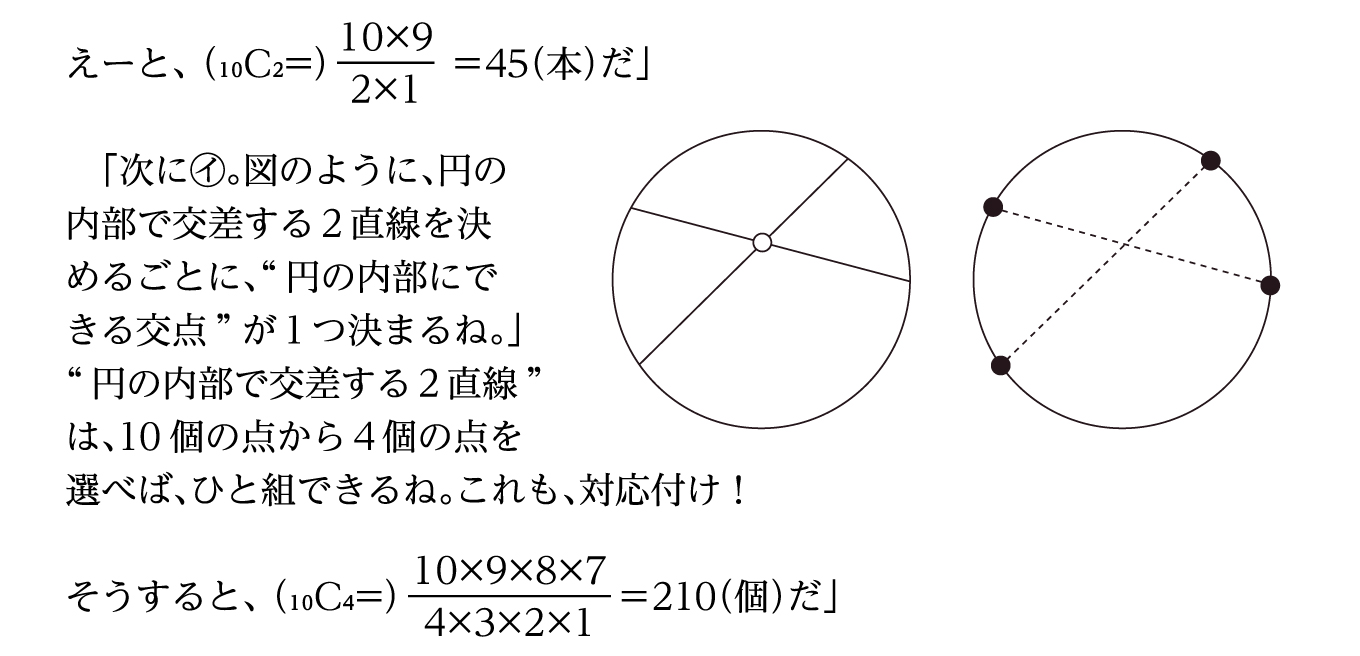
「“公式”によれば、この問題の答えは、45+210+1=256(個)となるね!」
ちょっと満足げな表情の生徒Aに、悪いとは思いつつ「君は、なぜこれで答えが出るのかを理解しているの?」と問いかけると、「あっ…いや…知りません。ただ、これを覚えておくように言われただけです」
すこし背筋が寒くなりました。生徒Aには罪はありません。これをただ「覚えておきなさい」と言った大人(講師)の罪深さにぞっとしてしまったのでした。
ここからは、その後の授業での私の解説です。こちらもやや省略気味です。
いま、既に3本の直線が引かれている図を想像しよう(下図1)。そこに、点線のような直線を新たに引く(図2)と、円の領域は増えるよね。いくつ増える?すでに引かれていた直線と交わるごとに1個ずつ増え、さらに、円から突き抜ける瞬間に1個増える(図3)よね。つまり、次々に直線を引くにつれ、「それまでの直線と交わる回数(図3の○)+1(図3の△)」だけ領域は増えて行くんだ。
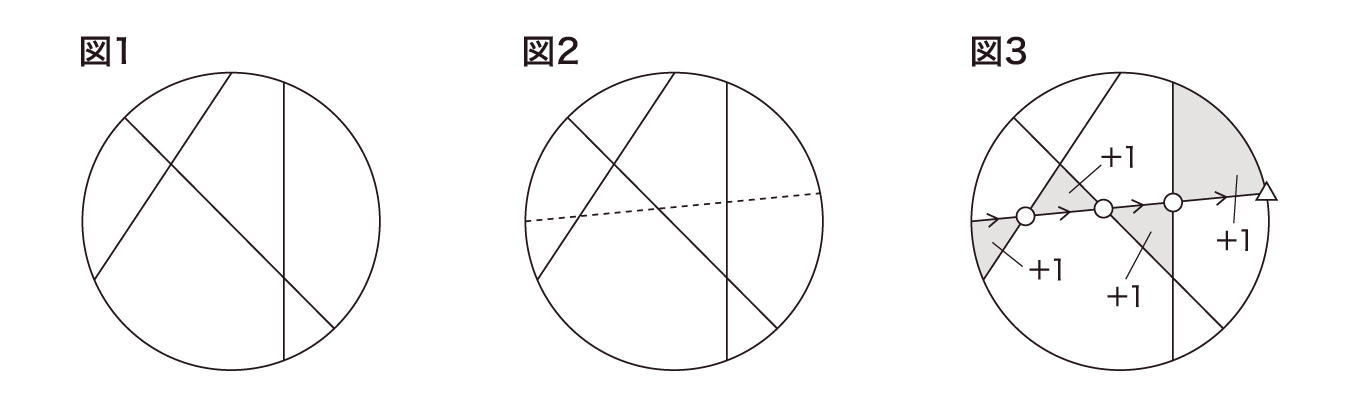
直線が1本も引かれていない(最初の)状態では、円の領域は1個だ。続けて1本ずつ直線を引いていくと、「新たにできる交点+1」ずつ領域は増えていくから、最後、45本目の直線を引き終えたときの領域の総数は、
1+(円の内部にできる交点の数)+45
最後の“45”は、って? 点下線(......)部の「+1」が引いた直線の数(45本)だけ現れるからだ。また、「どの3本も1点では交わりませんでした」という条件は、地味だけれど欠かせないものだよ。新たに引いた直線がそれまでに出来ている交点を通っても、その点を通る3本の直線によっては領域は囲めないからね…。
[実際の授業では、次のように文字を用いて、式を作って解説します。]

「理解できたかい? 波下線(~~~)部が㋑にあたり、二重下線(===)部が㋐にあたるわけだね。」
「はい、とてもよく分かりました。そして、分かって嬉しいです」
「僕はね、ただ覚えておけと言われた事柄を、今もなお覚えていた君の記憶力には敬服しますが、これからは、訳も分からず覚え込むような学びとはサヨナラをしてほしいと願っています。場合によっては、そのときには結局分からずじまいになることだってあるかも知れないけれど、いずれ、多くのことを学んで知識が増えれば、きっと理解できる瞬間が訪れますよ。」
あらゆる分野でどんな問いかけにも応えてくれる、ChatGPTをはじめとする生成AIが出現した世の中にあって、人間が自ら考えて答えにたどり着くというプロセスの価値が揺らぎ出している、というふうにも見えます。しかし、人工知能には答えは出せても価値を創造することができない、少なくとも、出した答えに価値を見出すことはできません。「覚えておけ」とはまさに、生成AIがやっている知識の受け売りにすぎません。君たちは、自分で考えて得た結論にこそ価値を感じることができるのです。
中学校で、新たに「数学」が始まります。君たちがもし「すべてを覚えてしまえばよい」式の学習を続ければ、数学は、君たちの味方になってはくれません。授業や本で必要最小限のことを学んだあとは、今度は自分をさらけ出して考えてください。そうすれば、心から数学を楽しめる日々が訪れることでしょう。
なお念のため書き添えれば、これは、生成AIに書かせた文章ではありません。生成AIならば、表向き、もっと気の利いた文章を作るでしょう(笑)。
