中学校からは、小学校とは違う新しい勉強が始まります。算数は数学という新しい教科に変わります。問題を考えるのに、算数ではごく限られた道具しか使えないのに対し、数学では格段に多い道具を手に入れて、より高度な問題を楽しめるようになります。まずは、道具を正しく身につけることをを目標にしましょう。


次は、中学入試を少し改題したものです。
問
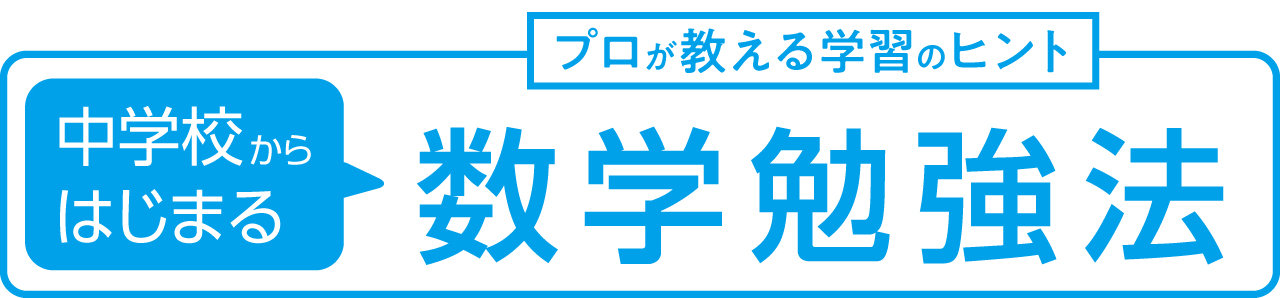
下の図のような、角Aが直角の直角三角形ABCがあり、辺BCの長さは13cmで、辺ABと辺ACの長さの和は17cmです。このとき、三角形ABCの面積を求めなさい。
3辺の長さが整数の比で表される直角三角形として有名な“5:12:13型”を知っている人ならば、簡単に、5×12÷2=30 (cm2) と答えるでしょう。でも、これでは「知っていたから解けた」に過ぎません。
では、知らなかったらお手上げか?……イヤイヤ、うまい手は、あります。
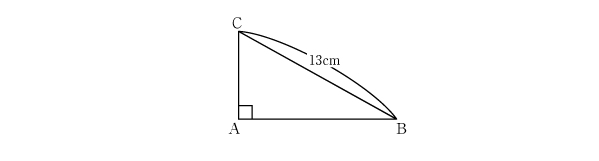
下の図のように、三角形ABCと合同な4つの三角形を用いて1辺の長さが17cmの正方形PQRSを囲むことができるから求める面積は、(17×17-13×13)÷4=30 (cm2)
難易度が高い発想ですね! こんなこと、思い付かないよ……という人もいるでしょう。
中学受験の算数の世界では、このように、「あらかじめ知っていた人」「難易度が高い発想ができた (または、この発想すら、経験により知っていた) 人」が「スッゴーイ!!」ともてはやされる場面が多いので、いきおい、経験値を高める学習が重要視されるのです。
数学においてもそういう学習は必要ですが、それよりも、問題を解くための道具立てを体系的に整備し、「確実に解く」ことができる範囲を広げることがより大切になります。
数学では、「文字式」を使いこなせるようにして、図形分野では、たとえば直角三角形において成り立つ「三平方の定理」を学びます。
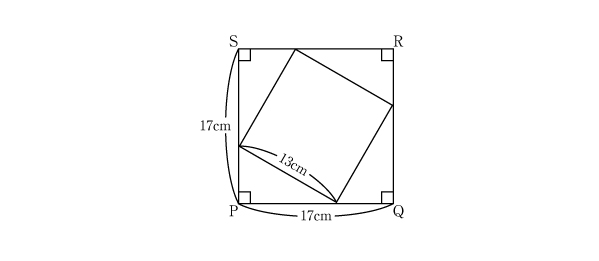
すると、算数ではできなかった
x+y=17
x×x+y×y=13×13
(うしろの式は、数学では、x2+y2=132)の関係式がたちどころにできます。
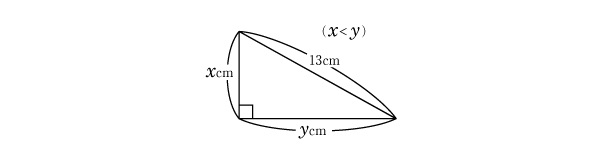
あとはこれらを満たすxとyの値を、これまた新たに学ぶ「2次方程式」を解く手順に従って、x=5、y=12と求めることができます。
つまり、何ら特殊な発想を要することなく、30cm2という答えにたどりつくことができるのです。
このことだけをとってみれば、数学という科目は、なんだか味気のないものに見えるかもしれませんね。しかし、心配は要りません!
問題を解決するための道具を充実させることで、小学生の頃には難問に見えた問題の多くが簡単に (?) 解決するようになる一方、これらの道具をもってしてもなお、解くのが難しい問題がたくさん現れてきます。
しかも、それらの中には、(とくに高校では)具体的に図や表で理解できる範囲を超えた、抽象的な内容を含むものもあります。
これらと向き合うことで、算数とは一味違うワクワク感を数学で体験できることでしょう。
上に書いたように、経験値を高める学習は数学においてもなお重要ですが、大事なのは、たとえば100の経験を、バラバラにではなく、10の大きな共通するテーマを持つグループに分類して頭の中の引き出し (あるいはノート) に整理することです。互いにリンクする情報は、つながった状態で理解しておいた方が記憶によく残りますし、有用です。
正負の数、文字式、方程式、……と中学で次々に学ぶ数学の単元から、道具を着実に手に入れて、それらを武器に自らの思考力を存分に試せる日々が続きますように。
数学を楽しんでください!!
